Difference between revisions of "Muon"
| Line 35: | Line 35: | ||
However, as the muons propagate with a velocity close to the speed of light, a relativistic correction to this calculation has to be applied. Namely, the mean lifetime has to be '''Lorentz transformed''' to the reference frame of a ''stationary'' observer (stationary with respect to Earth). | However, as the muons propagate with a velocity close to the speed of light, a relativistic correction to this calculation has to be applied. Namely, the mean lifetime has to be '''Lorentz transformed''' to the reference frame of a ''stationary'' observer (stationary with respect to Earth). | ||
| + | |||
| + | <math>\gamma = \frac{1}{\sqrt{1 - v^2/c^2}}</math> | ||
Revision as of 18:33, 17 April 2020
A muon (μ) is an elementary particle with unit electric charge and a mass of about 106 MeV/c2. Muons have a mean lifetime of about 2.2 μs and decay primarily into electrons and neutrinos.
Particle properties
Muons are elementary particles which interact graviationally, electromagnetically and weakly. The particles do not undergo strong interactions, owing to their half-integer spin. The mass of muons is about 106 MeV/c2, making them about 207 times heavier than electrons.
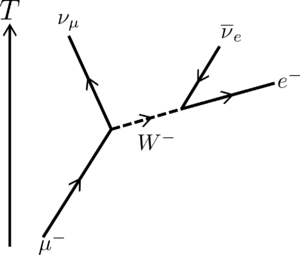
Muons have unit electric charge. Conventionally, muons (μ-) are considered to carry a negative charge, while their anti-matter counterparts (anti-muons or μ+) are positively charged. The weak interaction mediates the decay of muons. As weak processes can be considered slow on typical sub-atomic timescales, the muons exhibit a mean lifetime of about 2.2 μs. The most common decay products are electrons and neutrinos.
| Interactions | Gravity, Electromagnetic, Weak |
| Mass | 105.6583755(23) MeV/c2 |
| Mean lifetime | 2.1969811(22) x 10-6 s |
| Electric charge | 1 |
| Spin | 1/2 |
Muons in cosmic showers
Muons appear in cosmic showers as secondary shower particles. Owing to their finite lifetime t, the mean path of muonic shower particles is limited.
Classically, the mean path s is given by s = ct, assuming that the muons have a velocity close to the speed of light c. This expression yields a mean path of 660 m. Consequently, the large majority of cosmics shower muons would decay before they arrive at the surface of Earth.
However, as the muons propagate with a velocity close to the speed of light, a relativistic correction to this calculation has to be applied. Namely, the mean lifetime has to be Lorentz transformed to the reference frame of a stationary observer (stationary with respect to Earth).